Why you should avoid leveraged ETFs in the long run

Leveraged ETFs have grown in popularity through the years. According to ETF.com there are over 135 leveraged ETFs actively traded with the largest being ProShare UltraPro QQQ a.k.a. TQQQ, at $14.5 billion in assets. ProShares and Direxion are the most popular household names in the space.

Recently a new leveraged ETF is getting all the attention. A fund called TARK has sprung up providing a 2x leveraged position on ARKK, the infamous innovation technology ETF managed by Cathie Wood.

Now don’t get me wrong, market participants should have the freedom to make a variety of financial decisions through different competing investment products. That’s capitalism doing its job. But while I side with the principles of free market capitalism, as a long term investment, leveraged ETFs will only be a sure fire way to losses for the naïve investor. Let me explain.

2x

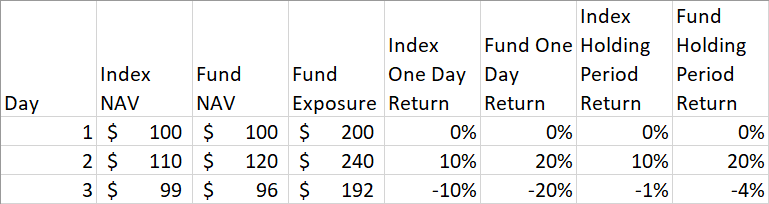
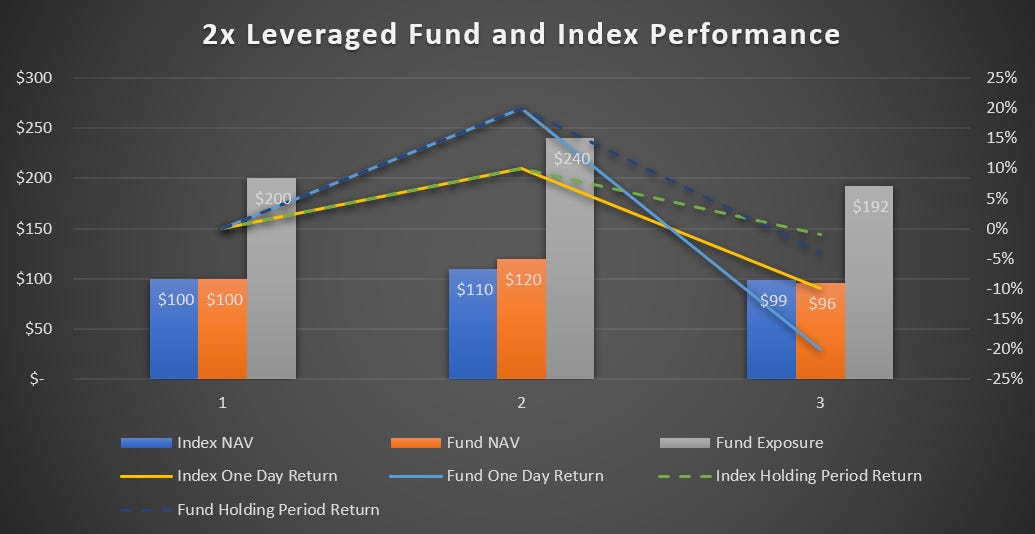
Let’s look at a 2x leveraged ETF that tracks an index over a 3 day market cycle.

We will assume the first day of trading the net asset value or NAV of both the index and leveraged fund is $100. In order to have 2x leverage, the fund will have to use swaps to increase its exposure. Two multiplied by $100 is $200 in exposure. Total exposure at the beginning of the day is now $200 for the fund, but remember the NAV of the fund is still $100.

On the second day let us assume the index increases by 10%. The NAV of the index is $110, but the NAV of the fund is now $120. Why? Because the fund had $200 exposure. Two hundred times a 10% return is $20. Therefore the original $100 NAV of the fund has increased by $20 to a NAV of $120. This is great! The fund is doing what is expected.

Now the NAV of the index is $110. The NAV of the leveraged fund is at $120, but in order to maintain a 2x exposure for the following day, the fund which originally had an exposure of $200 will now have to increase its swap exposure by $40. Why? Two times the $120 NAV of the fund is $240 of exposure. Two hundred forty dollars minus the original exposure of $200 is $40.

On the third day the index falls by 10%. The NAV of the index is now $99. The NAV of the leveraged fund on the other hand has decreased to $96. That is $240 times -10% is -$24. One hundred twenty dollars minus $24 is $96.

Over the course of the 3 days the index returned -1%. An inexperienced investor would assume a 2x leveraged fund would only lose -2%. In reality the leveraged fund lost -4%.

Lets do 3x and inverse it!

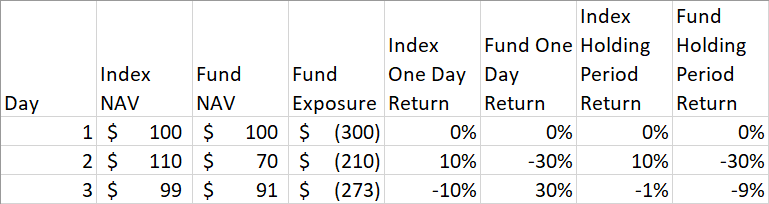
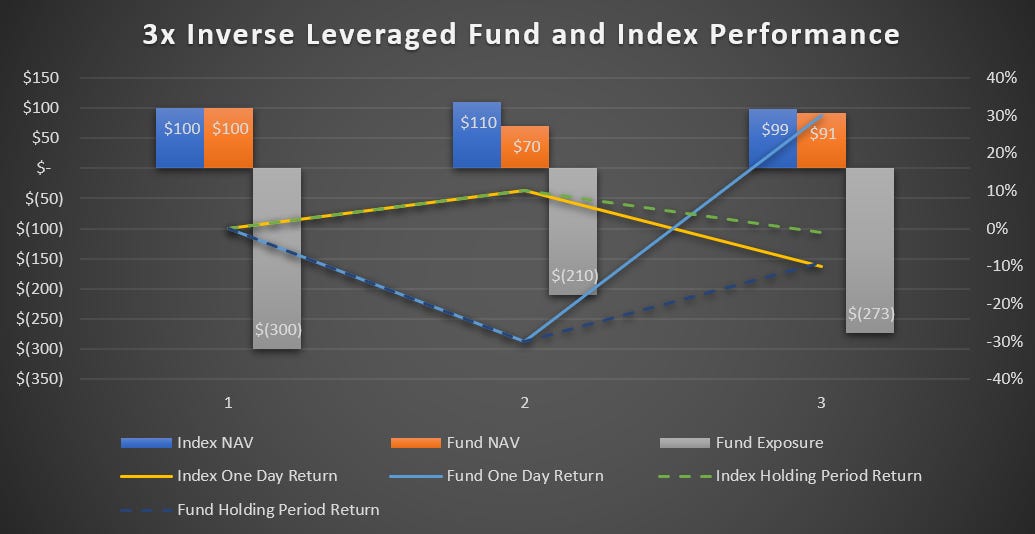
To make things even more interesting let’s look at a 3x leveraged inverse ETF that tracks an index over a 3 day market cycle.

Again we assume the first day of trading net asset value or NAV of both the index and leveraged fund is $100. In order to have negative 3x leverage, the fund will have to use swaps to increase its negative exposure. Negative 3 multiplied by $100 is -$300 hundred exposure. Total exposure at the beginning of the day is now -$300 for the fund, and remember the NAV of the fund is still $100.

On the second day the index increases by 10%. The NAV of the index increases to $110, but the NAV of the fund is now $70. Why? Because the fund had negative $300 exposure. Negative $300 times a 10% return is -$30. Therefore the original $100 NAV of the fund has fallen by $30 to a NAV of $70. Okay no surprise here, the fund is doing what is expected.

Now the NAV of the index is $110. The NAV of the leveraged fund is at $70, but in order to maintain a negative 3x exposure for the following day the fund which originally had an exposure of -$300 will now have to reduce its swap exposure by $90. Negative 3 times $70 is -$210 of exposure. Negative $210 minus the original exposure of -$300 is $90.

On the third day the index falls by 10%. The NAV of the index is now $99. The NAV of the inverse leveraged fund on the other hand has increased to $91. That is -$210 times -10% is $21. Seventy dollars plus $21 is $91.

Over the course of the 3 days the index returned -1%. A naïve investor would assume a 3x inverse leveraged fund would return 3%. In reality the leveraged fund lost -9%.

I hope this math proves my point to avoid these types of funds as long term investments. Happy Investing!